|
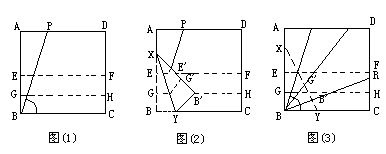
首先表明尺规法三等分任意角用高等数学已证明无解 然后折纸法比尺规法强大些,能三等分任意角(因为折纸破坏了尺规法定义) 步骤: (1)在一个正方形纸片上折出给出的角ang;PBC,将ABCD对折记折痕为EF;再将EBCF对折,折痕为GH(如图(1)); (2)翻折左下角使B重合在GH上记为Bprime;,且使E重合BP上记为Eprime;,点G折后的点记为Gprime;,折痕记为XY(见图(2)); (3)折B、G'和B、B',则BB'、BG'为ang;PBC的三等分线(见下图(3)).
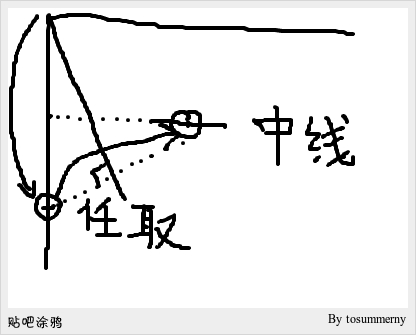
知识普及: 折纸中的直角等分 一般在折纸中用到的角等分都是以2或3的倍数等分直角,2只要不断对折直角即可 3等分角用到的是三十度角的正弦值为0.5这个知识 相当于用圆规截取直角边交于中线,两点连线的高即为直角三等分线
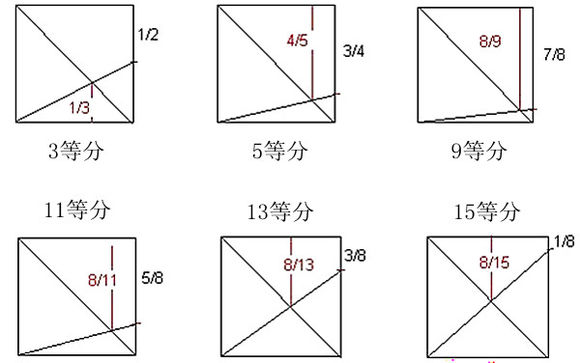
折纸中的边等分 偶数等分可以通过对折实现,如果不是2的纯倍数可通过除二算出奇数再使用奇数等分法 以下是比较简单易懂的一种:
向边上作高即可等分。用的是初中数学相似三角形的定理。 当然,把底边四等分强化到八等分的话,分别可得到9、11、13、15等分点
归纳可得:偶数等分的边连角截对角线得奇数等分 不过此法在高阶偶数上应用较为不便,还需灵活计算为宜。 这里介绍的仅仅是相似三角形等分法,多折神谷、老罗的作品能学到不少更高级的几何等分法。 |